Hello! It sure has been a while, huh? Here, have a coffee .

Today, I’ll be writing about the hidden magical gem that is Linear Programming, available in your nearest spreadsheet program, be it LibreOffice Calc, Excel, or Google Sheets.

---

Basics of Linear Programming

Unlike the other posts you might have seen within my blog, Linear Programming isn’t actually programming. Rather, it is “a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships”, according to Wikipedia.

For those who are uninitiated, or need a mini-not-so-professional-refresher, let us break down the definition.

A method to achieve the best outcome

Essentially, this is “optimization”. We construct an equation, and we try to either minimize or maximize it - you probably had some exposure to it in high school when they taught us how to differentiate.

However, in optimization, instead of figuring out if an equation should be minimized/maximized, we define if the equation should be minimized/maximized based on our requirements.

Whose requirements are represented by linear relationships

Linear relationships are essentially either equalities, or inequalities (=, >, < and so on):

An example of a linear inequality | Source: Me

Since the relationships must be linear, it implies that equations like the following cannot be solved with Linear Programming:

An example of a non-linear inequality | Source: Me

If inequalities like the above presents itself, the best course of action would be to use another kind of solver, like a nonlinear programming solver, or a Constraint Problem (CP) solver like this one by Google. However, chances are, that with a touch of creativity, most problems can be expressed as a linear programming problem.

Linear Programming

In a nutshell, given a bunch of inputs, lets say:

A bunch of inputs | Source: Me

We can define a bunch of constraints represented via linear relationships, like:

An example of a linear inequality | Source: Me

For Linear Programming involving only two variables, we can visualize how it works with graphs. Let’s say our two variables are x and y, and our constraints are:

First Constraint | Source: Me

Second Constraint | Source: Me

We will find that the graph on Desmos will look like this:

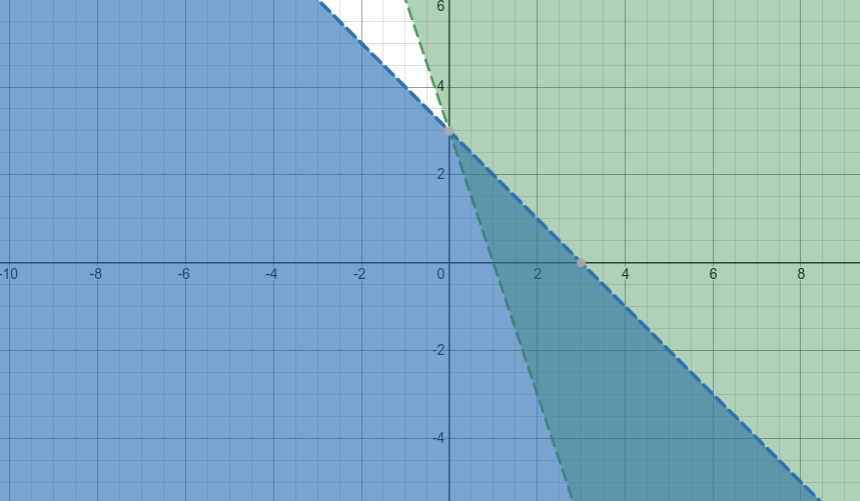
Graph. Green represents constraint 1, Blue represents constraint 2 | Source: Me

The intersected area (i.e. areas where both blue and green) are the solutions to the inequality (note that the intersection itself is not a solution, since both of our inequalities are not inclusive). Now, if we were to define an objective function, which is the function we want to minimize or maximize:

Objective Function, 2x + y | Source: Me

And then plot it on the graph:

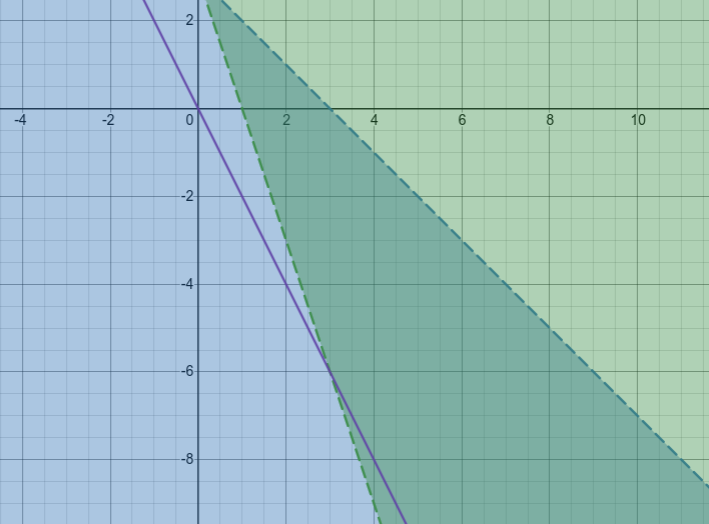
Objective Function (purple) on the graph | Source: Me

We see that the intersection between the line, and the overlapping shaded areas contain all the values that satisfies both constraints, and also the objective function. All we need to do now is to determine what x and y should be if we choose to maximize or minimize our objective function. If it was to maximize our objective function, then the answer we seek is as close to the intersection as possible. Otherwise, if we were to minimize our objective, then the answer we seek should technically be at another intersection, which isn’t possible with these particular constraints, hence, minimizing the objective would be “INFEASIBLE”.

To wrap up the example, performing linear programming would give us a few results:

• The value of x if the objective function was minimized/maximized
• The value of y if the objective function was minimized/maximized
• The value of the objective function after minimizing / maximizing

And subsequently, to wrap up generally:

• The value of x_1, x_2, x_3, ... x_n if the objective function was minimized/maximized
• The value of the objective function after minimizing / maximizing

With more variables, we are essentially working with linear constraints in n-dimensional graphs, which might sound difficult to visualize until you realize it doesn’t really matter, since the user is the one that defines the constraints anyway.

To learn more about how exactly to solve Linear Programming problems, look at the Simplex algorithm. Good solvers would indicate if there is more than one possible answer, or if there is a “close-enough” solution should the entire system be infeasible - although, that is in no way necessary or universal in well-used solvers.

---

Duty Planning

In my line of work (and probably most of yours, too), duty is a necessary part of work. As a software engineer, this could be translated to being on-call, as a doctor, it could be shifts to do ER, and so on. Needless to say, countless of psychological battles have been waged across the globe thanks to conflicts in agenda when it comes to planning for duty slots: “no weekends please”, or “no public holidays please”, or “my wife’s pregnant” or “I need to walk my pet rock”.

As a duty planner, if you were to ignore these claims, you would be seen as a cold-hearted human being. So I thought: why not just offload the work onto a computer program? Not only would this save time and be much fairer compared to a human (especially if you are also planning it yourself), you would be disguising your own stone-cold, immovable heart and instead blaming your inhumanness on a computer program.

Leveraging on Google Sheet’s integration with Google Forms, I modeled our own planning considerations as linear relationships, maximized preferred dates, and minimized the amount & quality (defined by weekends and public holidays) of duty disparity between each duty personnel. Then, I solved them using Google’s Linear Optimization Service (GLOS).

Originally, I used the OpenSolver app on Google Sheets to solve, but I later realized how slow it was when I was developing the Google Sheet.

Here is a GitHub snippet link that contains all of the Google Apps Script used within the relevant Google Sheet. The Google Sheet itself is not open-source, since it contains sensitive data that I won’t try cleaning.

Did you know that Google Sheet collaboration isn’t actually simultaneous? The edits from each user just happens so quickly that you see it as simultaneous. Not only is this due to JavaScript browser engines being incapable of multi-processing, but also based on personal experience, where a script can hog out all of the users when busy. Also, programmatically reading / writing each cell is extremely slow compared to bulk-writing an entire matrix into Google Sheets.

Instead, allow me to explain how I managed to create linear relationships for some of our planning considerations.

Take x_i_j (synonymous to x generally) to be any duty date where i and j is the personnel and day respectively, and b_i_j (synonymous to b generally) to be any backup date, where the personnel is to serve as a backup for the duty personnel.

1 represents duty / backup on that day (depending on whether x or b is referred to), and 0 represents no duty / backup on that day.

Set-In-Stone

As this is considered an “innovation” rather than an “invention”, it is meant to work as a transition between the old process (manually planning) to the new process (automatically planning). Hence, dates that are manually planted must not be changed. “Set-In-Stone” acquires non-empty cells, and adds a linear constraint for each affected cell:

• If there is a duty slot on that day, then x = 1, b = 0.
• If there is no duty slot on that day (forced), then x = 0, b = 0.
• If the person is meant to be a backup personnel, then x = 0, b = 1.

Daily personnel

Every single day should have 1 personnel performing duties, while another personnel will be the backup. This is achieved simply by summing for all i, in the same j, for all duties / backups.

Repeat this for every `j` | Source: Me

No consecutive days

If we were to generate a duty timetable now without some specific constraints, the model would simply assign all the duty to one single person who is free. There are three ways that we are combating this:

1. Ensuring that there are no consecutive days being served by any given person (in this sub-header);
2. Ensuring that everyone’s total points (sum of all of the days that they have served * a modifier based on weekend / public holiday) are close to the average points (pseudo-standard deviation, since we can’t break the linear property);
3. Ensuring that all personnel has a chance to do duty, based on the projected number of duty per personnel available in the date range.

For a single slot (i.e. the status of duty for a particular person on a particular day), consecutive days are prevented by using this clever little equation, iterating x_ij over all possible values of j for a number of days, where a is the limit to the number of days someone is allowed to serve.

Clever Sum | Source: Me

In effect, this ensures that a days after a duty / backup (not shown) slot, there will not be any more duties.

Roughly equal points

Without delving too deep into the point system details (as this is subjected to individual implementation), a common understanding between the planners and personnel involved alike are the roughly equal points that everyone should have.

As one of the pivotal factors to eliminate model bias, the points must be allocated fairly to each person. This is done quite simply by taking the projected amount of points (calculated by summing the possible points earned throughout the entire period, dividing by the number of days in the period), introducing a deviation variable, which dictates how many points can each person differ from one another, and then summing the points for each person, ensuring that it is between point_avg - deviation to point_avg + deviation.

Repeat this for every i | Source: Me

In effect, this means that the model itself would determine the value of deviation, which means that we want to minimize this as much as possible.

Backup & Actual Day cannot be on an unavailable date

This is actually quite simple. After plotting each unavailable date onto a matrix, the x and b just has to be 0 to 0 or 0 to 1, if unavailable or available respectively.

Backup & Actual Day cannot be on the same slot

This is also pretty simple. 0 < x + b < 1 would do the trick: x and b cannot both be 1, as that would result to 2, which is greater than 1. This prevents a person from simultaneously being his own backup.

Chance to do duty

This is done in two parts:

1. Everyone must do duty based on the projected average;
2. Everyone must do a weekday duty the equal number of times, based on projected average.

The constraints are quite simple:

1. Sum up everyone’s duty slots (barring points, all of j per i), and it must be greater or equal to the projected average;
2. Sum up everyone’s duty slots but only on the weekdays, and it must be greater or equal to the projected average.

Weekday is chosen solely due to the large availability compared to weekends - there may be less weekends than the amount of people you are planning for!

Unsaid Constraints

For obvious reasons, x and b can only either be 0 or 1. deviation is a continuous variable, solely because points can be expressed as decimals.

---

The Objective

Combined together, the objective of our function is to prioritize & maximize preferred slots (by modifying the points at the objective level, which has benefits over constraint level, as objective is suggestive, while constraints are requirements), while minimizing the deviation variable mentioned earlier.

In a nutshell we are maximizing:

Objective Function | Source: Me

where deviation and x is as expected, while s is a matrix containing values that are either 0, 1 or 2. 1 represents a normal day, while 2 represents a preferred day; 0 is essentially nil - since there is already a constraint that prevents duty slots from being filled if personnel is unavailable.

The result:

Beautiful Result | Source: Me

Green is duty, Yellow is backup, Black is unavailable, and Red is nothing. C is special consideration.

---

Conclusion

Before I learnt about optimization functions through a mathematical nerd friend of mine, I always thought this kind of problem would be easier solved with things like Machine Learning, or brute-force search.

However, optimization functions not only reduces the search-space by a lot, it also ensures that the result is mathematically sound, and a hundred percent cold and calculating so that you can freeze anyone who decides you are being too inhumane in planning. Or, you could be soft like me and add in dates of consideration (like ethnic holidays). Feel free to use my Google Apps Script code, that is, after you figure out how to create a Google Sheet that it requires as input!

Happy Coding,

CodingIndex